
[INMO-1995]: In an acute-angled traingle \(ABC\), \(\angle A = 30^0\), \(H\) is the orthocentre, and \(M\) is the midpoint of \(BC\). On the line \(HM\), take a point \(T\) such that \(HM = MT\). Show that \(AT = 2BC\).
Solution:
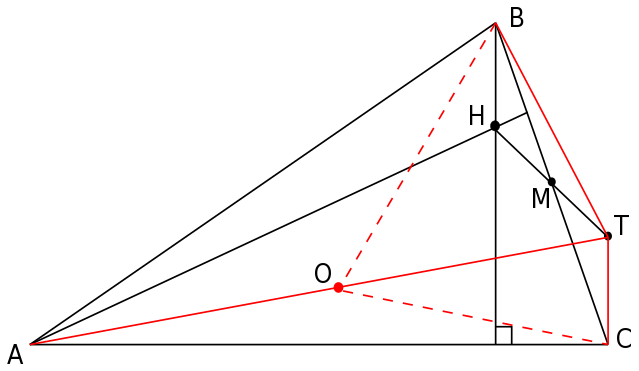
Since \(M\) is the midpoint of \(HT\) and \(M\) is also the midpoint of \(BC => BC\) and \(HT\) bisect each other. This implies that \(BHCT\) is a parallelogram; which makes \(BH\) parallel to \(TC\). Since \(BH \perp AC => TC \perp AC\). Similarly, \(TB \perp AB\).
The quadrilateral \(ACTB\) becomes a cyclic quadrilateral because \(\angle ABT + \angle ACT = 180^o\). Furthermore, since \(\angle ABT = \angle ACT = 90^o, AT\) is the diameter of the circumcircle of \(ACTB\).
Say we call the midpoint of \(AT\) as \(O\). Since \(AT\) is the diameter, \(O\) becomes the centre of the circumcircle of \(ACTB\). Since, \(\angle BAC = 30^o => \angle BOC = 60^o\). Since \(OB = OC\) (= radius of circumcircle), \(\triangle OBC\) becomes an equilateral triangle. Thus, the length of \(BC\) is same as the radius of the circumcircle which is half the diameter \(AT\).